Stéphane

Stéphane

I am a Ph.D. candidate in economics at Université de Montréal.

JMP - Long run carbon consumption risks and asset prices

Working paper, 2021

Slides Paper

Motivation

  • FIRST
    • Environnemental issues
    • Consumption of goods and services pollutes the environnement ;
    • Production vs. consumption-based CO2 emissions (GCP). Fact
    • Despite that, most papers and climate policies focus on the production side.
  • SECOND
    • Climate change is a long horizon phenomenon ;
    • Need a long-run risk model to assess it ;
    • Yet, the effect of the canonical long-run risks on the assets depends on investors detecting it ;
    • Require a new LRR model by considering carbon emissions consumption.
    • However, emission does have long-run risk and is more detectable :
    • Curbing carbon emissions at the pre-industrial level ;
    • Emission $\rightarrow$ Damages $\rightarrow$ affects aggregate consumption.

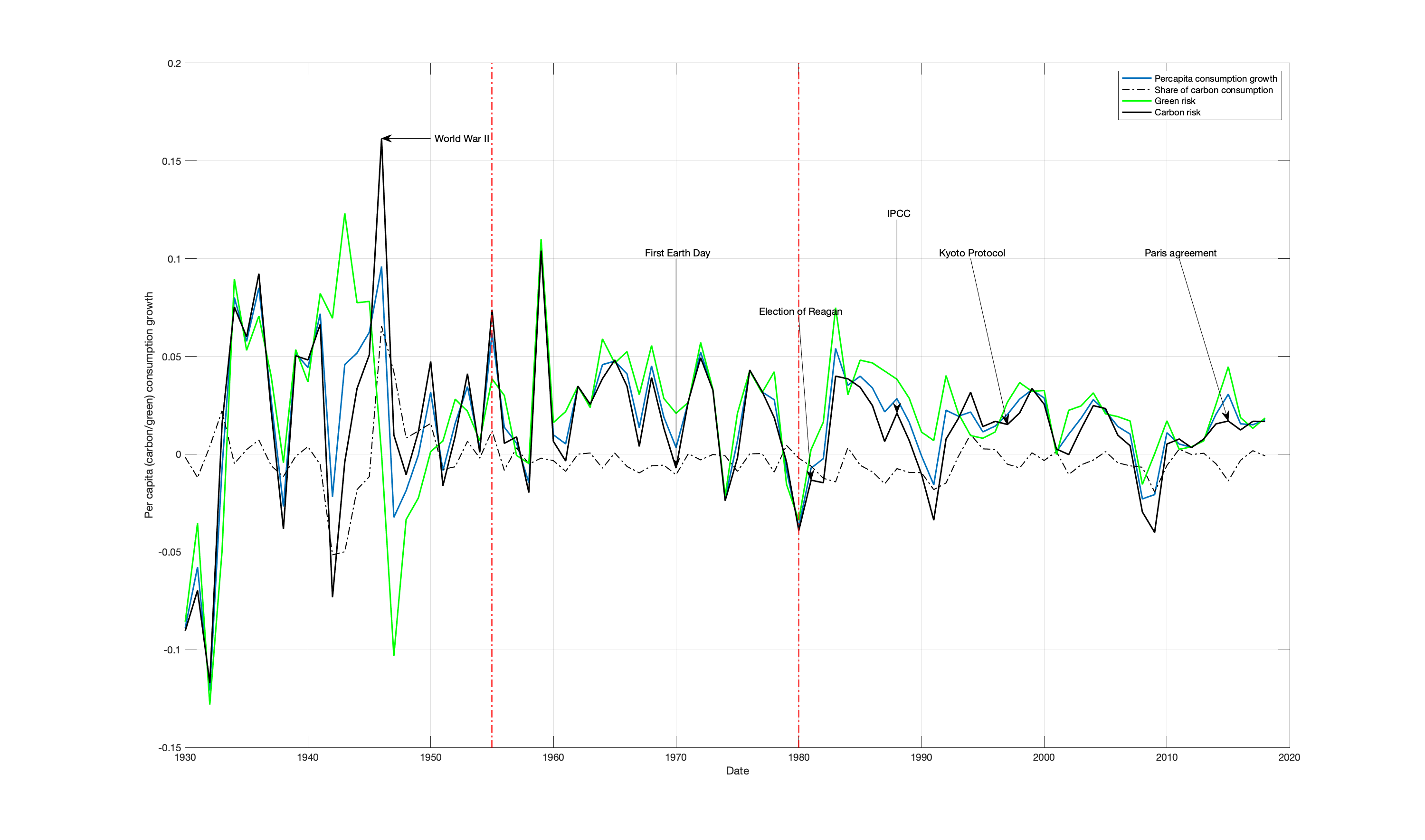
Data

MarineGEO circle logo

Model

Long-run carbon consumption risks model

  • Consumption growth decomposition :
$$\Delta c_{t+1} = \Delta cc_{t+1} - \Delta\alpha_{cc, t+1}$$
  • Carbon consumption growth dynamic :
$$\Delta cc_{t+1} = \nu_{cc} + x_t + \sigma_t \epsilon_{cc, t+1}$$
  • Conditional expectation of carbon consumption growth dynamic :
$$x_{t+1} = \rho_x x_t + \psi_x \sigma_t \epsilon_{x, t+1}$$
  • Conditional volatilty of carbon consumption growth dynamic :
$$\sigma_{t+1}^2 = (1 - \nu)\sigma^2 + \nu \sigma_t^2 + \sigma_w \epsilon_{\sigma, t+1}$$
  • Share of carbon consumption out of total consumption growth dynamic :
$$\Delta\alpha_{cc, t+1} = \nu_\alpha (1 - \rho_\alpha) + \rho_\alpha \Delta\alpha_{cc, t} + \sigma_\alpha \epsilon_{\alpha, t+1} + \pi \sigma_t \epsilon_{cc, t+1}$$
  • Dividend of any asset i growth dynamic :
$$\Delta d_{i, t+1} = \nu_i + \phi_i x_t + \phi_{\alpha, i} \Delta\alpha_{cc, t} + \psi_i \sigma_t \epsilon_{i, t+1}$$

Where $\epsilon_{x, t+1}, \epsilon_{cc, t+1}, \epsilon_{\alpha, t+1}, \epsilon_{i, t+1}$ and $\epsilon_{\sigma, t+1}$ are i.i.d.

Findings

  • LRCCR model replicates the equity premium, volatility and risk-free rate much better than LRR :
    • By decomposing consumption growth into two components ;
    • Long-run risks in both expected carbon consumption and volatility.
  • My LRCCR model increases the capacity to detect the long-run risk during the period 1956-2018. But during the period 1930 - 1955, it was less dectectable :
    • Investors can profit from it using climate change news ;
  • The long-run risk variable $x_t$ and its conditional variance $\sigma _t ^2$ help improving the predictability of the equity premium and the consumption growth.